Learning Rate Decay & Problem of Local Optima
Learning Rate Decay
One thing that may help speed up your learning algorithm is to slowly reduce your training rate over time. This is called learning rate decay. Suppose you're implementing mini-batch gradient descent, with a reasonably small mini-batch. Maybe a mini-batch has just 64, 128 examples. Then as you iterate, your steps will be a little bit noisy. And it will tend towards this minimum over here, but it won't exactly converge. But your algorithm might just end up wandering around, and never really converge, because you're using some fixed value for alpha.
α = α0 / (1+decayRate×epochNumber)α0 : initial learning rate
Other formulas for learning rate decay
Exponentially decay
α = α0 * 0.95^epochNumber
Discrete staircase
After a few iteration, make the learning rate to be half the initial learning rate.
Manual Decay
When training takes a long time, it can be continuously observed, and we can manually reduce the training rate.
Other
α = α0 * k / sqrt(epochNumber)
Problem of Local Optima
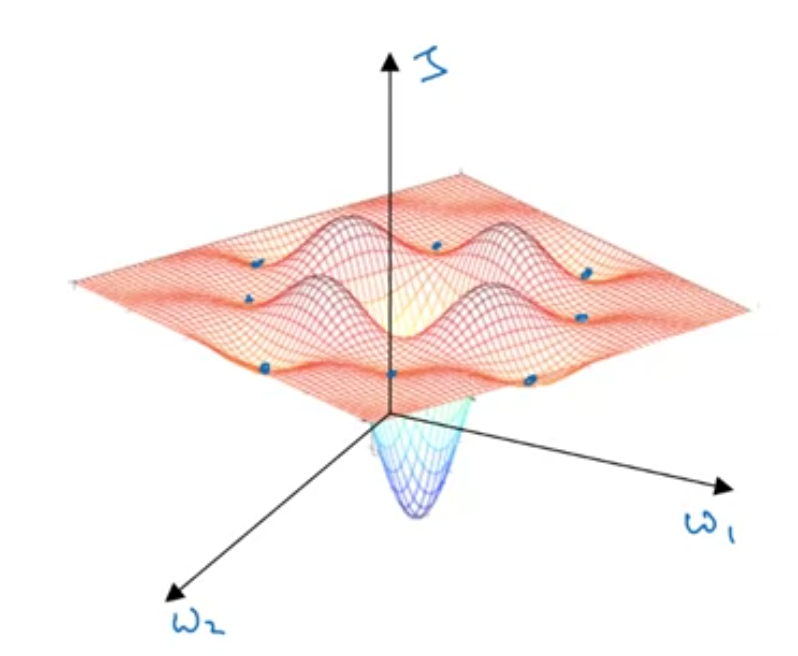
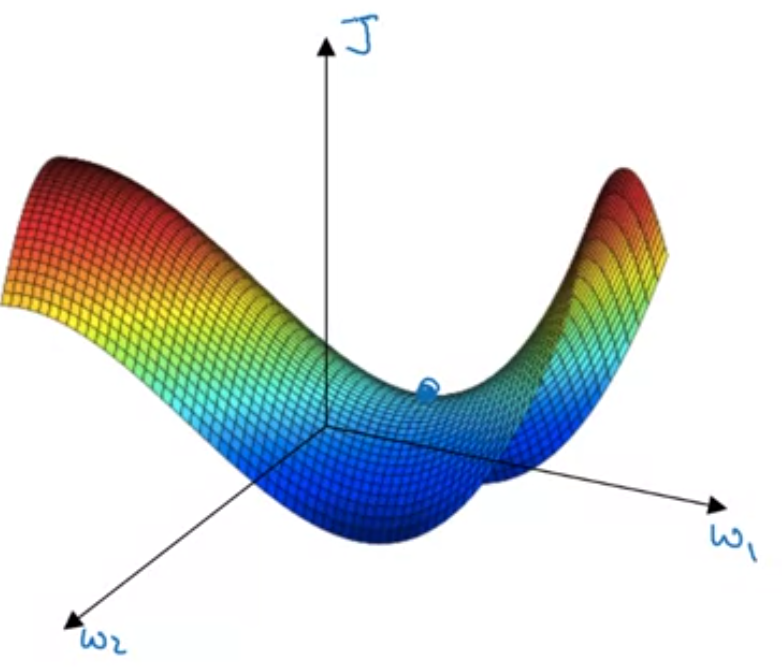
The above is what people think of when they complain about local optima. However, as deep learning advances, most points with zero gradient are not local optima like points like this. Instead, they are saddle points as shown below.
A function of very high dimensional space, if the gradient is zero, then in each direction it can either be a convex light function or a concave light function (u shape or n shape).
If you are in, say, a 20,000 dimensional space, then for it to be a local optima, all 20,000 directions need to look like U shape, which has small chances to happen.
So the takeaways are, you're actually pretty unlikely to get stuck in bad local optima so long as you're training a reasonably large neural network, save a lot of parameters, and the cost function J is defined over a relatively high dimensional space.
What's the problem then?
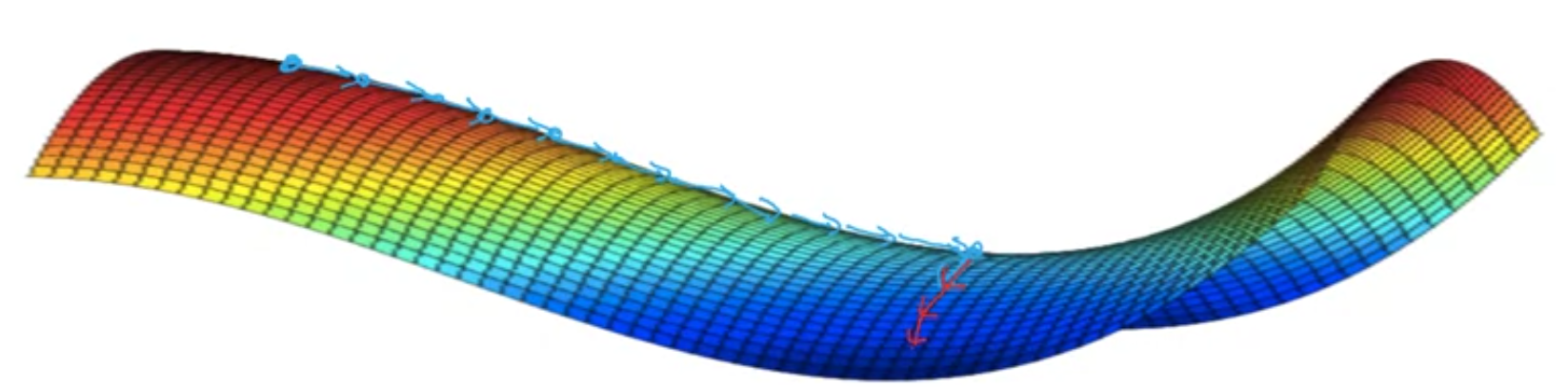
If local optima is not a problem, the problem is plateau. It will take this very long slope off before it's found its way to the optima and get off this plateau. This is where RMS prop and Adam can help to speed up the training.