Softmax regression

So far, the classification examples we've talked about have used binary classification, where you had two possible labels, 0 or 1. Is it a cat, is it not a cat? What if we have multiple possible classes? There's a generalization of logistic regression called Softmax regression. The less you make predictions where you're trying to recognize one of C or one of multiple classes, rather than just recognize two classes.

The output label y_hat would be in a dimension of (C,1) where C is the number of class and it denotes the probability of a given input belongs to a class. Therefore it should sum to 1. To ensure that it always sum to 1, we use the softmax function, which accepts a vector / matrix and compute the result.

The function is as shown below

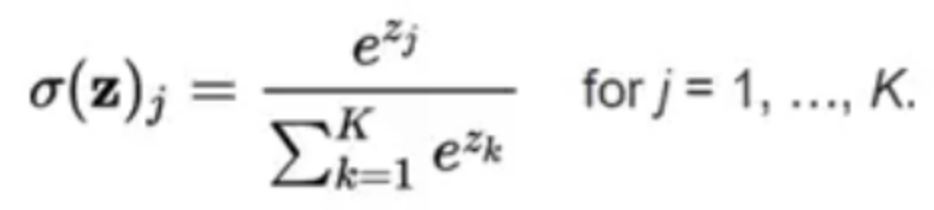
Training a softmax classifier

The name softmax comes from contrasting it with hard max, which means setting the highest value to 1 and the rest to be 0. When softmax's number of class is 2, it reduces to logistic regression.

Loss function

# Loss in one training data
L(y_hat, y) = - sum(y * log y_hat)
J = (1/m) * sum(L(y_hat, y))

Gradient descent

## Forward propagation
a[l] = softmax(z[l])
## Back propagation
dz[l] = y_hat - y

On other layer, it is computed similarly.